Superficie de fluencia

La superficie de fluencia de un material es una construcción abstracta que permite visualizar el conjunto de tensiones posibles o admisibles dentro de un sólido deformable elastoplástico.
Introducción[editar]
El estado tensional de un sólido deformable puede caracterizarse mediante tres valores de tensión según tres direcciones perpendiculares conocidas como tensiones principales de tensión, siendo los tres valores de tensión las llamadas tensiones principales. Por eso así el estado tensional en ese punto puede representarse por un espacio tridimensional . La superficie de fluencia es una superficie bidimensional en dicho espacio de tensiones.
Cuando un sólido deformable se somete a tensiones progresivamente mayores, la energía potencial elástica se incrementa y a partir de cierto punto se producen transformaciones termodinámicas irreversibles al superar dicha energía cierto valor. El conjunto de puntos por debajo de los cuales no se producen transformaciones termodinámicas irreversibles es el conjunto de tensiones admisibles es una región conexa del espacio de tensiones. La frontera de la región de tensiones admisibles es precisamente superficie de fluencia.
Plasticidad perfecta[editar]
Un material elastoplástico se dice que presenta plasticidad perfecta, si sea cual sea el valor de las tensiones en un punto, la superficie de fluencia no cambia ni de forma ni de posición en el espacio abstracto de tensiones. Cuando un material presenta plasticidad perfecta las ecuaciones constitutivas no necesitan incluir variables internas ni esfuerzos conjugados asociados y el problema elastoplástico es más sencillo.
Los materiales reales sin embargo casi siempre presentan plasticidad imperfecta, y la superficie de fluencia puede sufrir desplazamientos, tal como sucede en el efecto Bauschinger. Los cambios de forma, generalmente están asociados al comportamiento de endurecimiento, aumentando en ese caso el volumen encerrado en la superficie de fluencia.
Propiedades de la superficie de fluencia[editar]
- Convexidad. Bajo argumentos termodinámicos puede probarse que, La superficie de fluencia es convexa.[1]
- Compacidad. La superficie de fluencia se considera cerrada y por tanto encierra un volumen finito. Y por tanto el conjunto de tensiones alcanzables es siempre un conjunto compacto.
- Continuidad. La superfiecie de fluencia se considera que es Lipshitz-continua.
- Unicidad del problema elastoplástico. Cuando la superficie no es diferenciable el problema elastoplástico puede ser tratado mediante métodos variacionales. Bajo condiciones suficientemente regulares puede probarse que la solución del problema elastoplástico, aun cuando la superficie no sea diferenciable, es única.[2]
Ejemplos[editar]
Hay varias superficies de fluencia diferentes conocidas en ingeniería y las más populares se enumeran a continuación.
Superficie de fluencia de Tresca[editar]
El criterio de fluencia de Tresca se considera obra de Henri Tresca.[3] También se conoce como "teoría tensión cortante máxima" (MSST) y criterio Tresca-Guest[4] (TG). En términos de las tensiones principales el criterio de Tresca se expresa como
Donde es el límite elástico en corte y es el límite elástico en tracción.
La Figura 1 muestra la superficie de fluencia de Tresca-Guest en el espacio tridimensional de tensiones principales. Es un prism de seis lados y de longitud infinita. Esto significa que el material permanece elástico cuando las tres tensiones principales son aproximadamente equivalentes (un hidrostática), sin importar cuánto se comprima o estire. Sin embargo, cuando una de las tensiones principales se vuelve menor (o mayor) que las demás, el material está sujeto a corte. En tales situaciones, si el esfuerzo cortante alcanza el límite elástico, entonces el material ingresa al dominio plástico. La Figura 2 muestra la superficie de fluencia de Tresca-Guest en un espacio de tensiones bidimensional, es una sección transversal del prisma en el plano .


Superficie de fluencia de von Mises[editar]
El criterio de fluencia de von Mises se expresa en las tensiones principales como
donde es el límite elástico en tensión uniaxial.
La Figura 3 muestra la superficie de fluencia de von Mises en el espacio tridimensional de tensiones principales. Es un cilindro de base circular de longitud infinita con su eje inclinado en ángulos iguales a las tres tensiones principales. La Figura 4 muestra la superficie de fluencia de von Mises en un espacio bidimensional en comparación con el criterio de Tresca-Guest. Una sección transversal del cilindro de von Mises en el plano de produce la forma elliptical de la superficie de fluencia.


Criterio de Burzyński-Yagn[editar]
Este criterio toma la forma[5][6]
y representa la ecuación general de una superficie de revolución de segundo orden alrededor del eje hidrostático. Algunos casos especiales son:[7]
- Cilindro (Maxwell (1865), Huber (1904), von Mises (1913), Hencky (1924)),
- Cono (Botkin (1940), Drucker-Prager (1952), Mirolyubov (1953)),
- Paraboloide (Burzyński (1928), Balandin (1937), Torre (1947)),
- Elipsoide centrado en el plano de simetría , (Beltrami (1885)),
- Elipsoide centrado en el plano de simetría con (Schleicher (1926)),
- Hiperboloide de dos hojas (Burzynski (1928), Yagn (1931)),
- Hiperboloide de una hoja centrada en el plano de simetría , , (Kuhn (1980))
- Hiperboloide de una hoja , (Filonenko-Boroditsch (1960), Gol'denblat-Kopnov (1968), Filin (1975)).
Las relaciones compresión-tensión y torsión-tensión se pueden calcular para
Las relaciones de Poisson en tensión y compresión se obtienen usando
Para materiales dúctiles la restricción
es importante. La aplicación de criterios rotacionalmente simétricos para falla frágil con
no ha sido suficientemente estudiado.[8]
El criterio de Burzyński-Yagn es muy adecuado para fines académicos. Para aplicaciones prácticas, se debe introducir en la ecuación el tercer invariante del desviador en potencia par e impar, por ejemplo:[9]
Criterio de Huber[editar]
El criterio de Huber consta del elipsoide de Beltrami y un cilindro de von Mises escalado en el espacio de tensión principal,[10][11][12][13] ver también[14][15]
con . La transición entre las superficies en la sección transversal es continuamente diferenciable. El criterio representa la "visión clásica" con respecto al comportamiento material inelástico:
- comportamiento del material sensible a la presión para con y
- comportamiento del material insensible a la presión para con
El criterio de Huber se puede utilizar como superficie de fluencia con una restricción empírica para el índice de Poisson en la tensión , lo que conduce a .
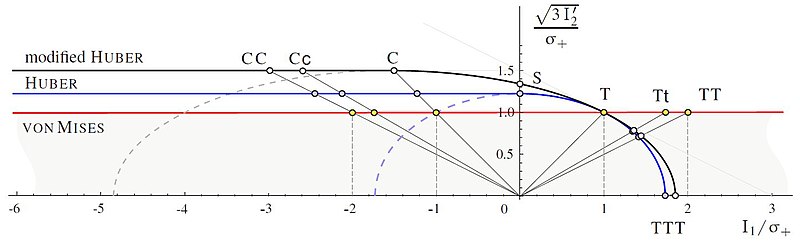
El criterio de Huber modificado,[16][15] ver también,[17] cf.[18]
Consiste en el elipsoide de Schleicher con la restricción del índice de Poisson en compresión
y un cilindro con la transición en la sección transversal . La segunda configuración de los parámetros y sigue con la relación compresión/tensión
El criterio de Huber modificado se puede adaptar mejor a los datos medidos como el criterio de Huber. Para configurar sigue y .
El criterio de Huber y el criterio de Huber modificado deben preferirse al criterio de von Mises, ya que se obtienen resultados más seguros en la región . Para aplicaciones prácticas, en estos criterios se debe considerar el tercer invariante del desviador .[15]
Superficie de fluencia de Mohr-Coulomb[editar]
El criterio de fluencia (fallo) de Mohr-Coulomb es similar al criterio de Tresca, con disposiciones adicionales para materiales con diferentes límites elásticos a tracción y compresión. Este modelo se utiliza a menudo para modelar hormigón, suelos o materiales granulares. El criterio de fluencia de Mohr-Coulomb se puede expresar como:
donde
y los parámetros y son los esfuerzos de fluencia (fallo) del material en compresión y tensión uniaxial, respectivamente. La fórmula se reduce al criterio de Tresca si .
La Figura 5 muestra la superficie de fluencia de Mohr-Coulomb en el espacio tridimensional de tensiones principales. Es un prisma cónico y determina el ángulo de inclinación de la superficie cónica. La Figura 6 muestra la superficie de fluencia de Mohr-Coulomb en un espacio de tensión bidimensional. En la Figura 6, y se utilizan para y , respectivamente, en la fórmula. Es una sección transversal de este prisma cónico en el plano de . En la Figura 6, Rr y Rc se utilizan para Syc y Syt, respectivamente, en la fórmula.


Superficie de fluencia Drucker-Prager[editar]
El Drucker–Prager yield criterion es similar al criterio de fluencia de von Mises, con disposiciones para el manejo de materiales con diferentes límites elásticos a la tracción y a la compresión. Este criterio se utiliza con mayor frecuencia para hormigón, donde tanto los esfuerzos normales como los de corte pueden determinar la falla. El criterio de fluencia de Drucker-Prager puede expresarse como
donde
y , son los esfuerzos de fluencia uniaxiales en compresión y tensión respectivamente. La fórmula se reduce a la ecuación de von Mises si .
La Figura 7 muestra la superficie de fluencia de Drucker-Prager en el espacio tridimensional de tensiones principales. Es un cone normal. La Figura 8 muestra la superficie de fluencia de Drucker-Prager en un espacio bidimensional. El dominio elástico elíptico es una sección transversal del cono en el plano de ; se puede elegir para cruzar la superficie de cedencia de Mohr-Coulomb en diferente número de vértices. Una opción es intersecar la superficie de fluencia de Mohr-Coulomb en tres vértices a cada lado de la línea , pero generalmente se seleccionan por convención para que sean aquellos en el régimen de compresión.[19] Otra opción es intersecar la superficie de cedencia de Mohr-Coulomb en cuatro vértices en ambos ejes (ajuste uniaxial) o en dos vértices en la diagonal (ajuste biaxial).[20] El criterio de fluencia de Drucker-Prager también se expresa comúnmente en términos de la cohesión del material y del ángulo de fricción.


Superficie de fluencia Bresler-Pister[editar]
El criterio de fluencia de Bresler-Pister es una extensión del criterio de fluencia de Drucker-Prager que utiliza tres parámetros y tiene términos adicionales para materiales que ceden bajo compresión hidrostática. En términos de las tensiones principales, este criterio de fluencia se puede expresar como:
donde son constantes materiales. El parámetro adicional le da a la superficie de fluencia una sección transversal ellipsoidal cuando se ve desde una dirección perpendicular a su eje. Si es el límite elástico en compresión uniaxial, es el límite elástico en tensión uniaxial y es el límite elástico en compresión biaxial, los parámetros se pueden expresar como:


Superficie de fluencia Willam-Warnke[editar]
El criterio de fluencia de Willam-Warnke es una versión suavizada con tres parámetros del criterio de fluencia de Mohr-Coulomb que tiene similitudes en la forma con los criterios de fluencia de Drucker–Prager y de Bresler-Pister.
El criterio de fluencia tiene la forma funcional
Sin embargo, se expresa más comúnmente en coordenadas Haigh-Westergaard como
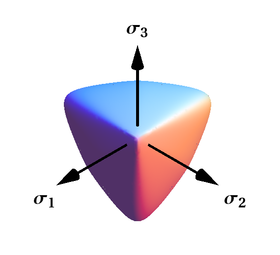
La sección transversal de la superficie vista en su eje es un triángulo suavizado (a diferencia de Mohr-Coulomb). La superficie de cedencia de Willam-Warnke es convexa y tiene derivadas primera y segunda únicas y bien definidas en cada punto de su superficie. Por lo tanto, el modelo de Willam-Warnke es computacionalmente robusto y se ha utilizado para una variedad de materiales cohesivo-friccionales.


Superficies trigonométricas de fluencia de Podgórski y Rosendahl[editar]
Normalizado con respecto a la tensión de tracción uniaxial , el criterio de Podgórski[21] en función del ángulo de tensión afirma que
con la función de forma de simetría trigonal en el plano
Contiene los criterios de von Mises (círculo en el plano , , ), Tresca (hexágono regular, , ), Mariotte (triángulo regular, , ), Ivlev[22] (triángulo regular, , ) y también el criterio cúbico de Sayir[23] (el criterio de Ottosen[24]) con y los hexágonos isotoxales (equiláteros) del criterio de Capurso[22][23][25] con . La transición von Mises - Tresca[26] se sigue con , . Los hexágonos isogonales (equiangulares) del criterio de Haythornthwaite[15][27][28] que contienen el criterio de Schmidt-Ishlinsky (hexágono regular) no se pueden describir con el criterio de Podgórski.
El criterio de Rosendahl[29][30] dice que
con la función de forma de simetría hexagonal en el plano
Contiene los criterios de von Mises (círculo, , ), Tresca (hexágono regular, , ), Schmidt-Ishlinsky (hexágono regular, , ), Sokolovsky (dodecágono regular, , ), y también el criterio bicúbico[15][29][31][32] con o igualmente con y los dodecágonos isotoxales del criterio de fluencia unificado de Yu[33] con . Los dodecágonos isogonales del criterio multiplicativo ansatz de simetría hexagonal[15] que contienen el criterio de Ishlinsky-Ivlev (dodecágono regular) no pueden ser descrito por el criterio de Rosendahl.
Los criterios de Podgórski y Rosendahl describen superficies individuales en el espacio de tensiones principal sin contornos exteriores adicionales ni intersecciones planas. Tenga en cuenta que para evitar problemas numéricos, la función de parte real se puede introducir en la función de forma: y . La generalización en la forma [29] es relevante para investigaciones teóricas.
Se puede obtener una extensión sensible a la presión de los criterios con la sustitución lineal [15]
lo cual es suficiente para muchas aplicaciones, como por ejemplo diversos metales, hierro fundido, aleaciones, hormigón, polímeros no reforzados y otros.

Superficie de fluencia Bigoni-Piccolroaz[editar]
El criterio de fluencia de Bigoni-Piccolroaz[34][35] es una superficie de siete parámetros definida por
donde es la función "meridiano"
que describe la sensibilidad a la presión y es la función "desviatoria"[36]
describiendo la dependencia de Lode de la fluencia. Los siete parámetros materiales no negativos son:
definiendo la forma de las secciones de meridianos y desviadores.
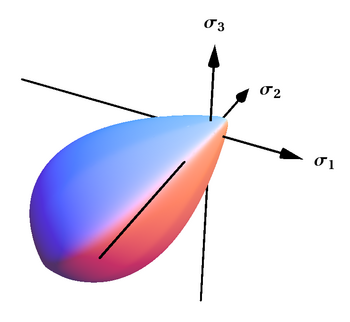
Este criterio representa una superficie lisa y convexa, que está cerrada tanto en tensión como en compresión hidrostática y tiene una forma de gota, especialmente adecuada para describir materiales granulares y de fricción. Este criterio también se ha generalizado al caso de superficies con esquinas.[37]
Coseno Ansatz (Altenbach-Bolchoun-Kolupaev)[editar]
Para la formulación de los criterios de resistencia, se puede usar el ángulo de tensión:
El siguiente criterio de comportamiento del material isotrópico
contiene una serie de otros criterios menos generales bien conocidos, siempre que se elijan valores de parámetros adecuados.
Los parámetros y describen la geometría de la superficie en el plano . Están sujetos a las restricciones
que se siguen de la condición de convexidad. En[38][39] se propone una formulación más precisa de la tercera restricción.
Los parámetros y describen la posición de los puntos de intersección de la superficie de fluencia con el eje hidrostático (espacio diagonal en el espacio de tensión principal). Estos puntos de intersección se denominan nodos hidrostáticos. En el caso de materiales que no fallan a presión hidrostática (acero, latón, etc.) se obtiene . De lo contrario, para materiales que fallan ante la presión hidrostática (espumas duras, cerámicas, materiales sinterizados, etc.), se sigue que .
Las potencias enteras y , describen la curvatura del meridiano. El meridiano con es una línea recta y con es una parábola.
Superficie de fluencia de Barlat[editar]
Para los materiales anisotrópicos, dependiendo de la dirección del proceso aplicado (por ejemplo, laminado), las propiedades mecánicas varían y, por lo tanto, es crucial utilizar una función de fluencia anisotrópica. Desde 1989 Frédéric Barlat desarrolló una familia de funciones de fluencia para el modelado constitutivo de la anisotropía plástica. Entre ellos, el criterio de fluencia Yld2000-2D se ha aplicado para una amplia gama de láminas metálicas (por ejemplo, aleaciones de aluminio y aceros avanzados de alta resistencia). El modelo Yld2000-2D es una función de fluencia de tipo no cuadrático basada en dos transformaciones lineales del tensor de tensión:
- donde es la tensión efectiva y y son las matrices transformadas (mediante transformación lineal C o L):
- donde s es el tensor de tensión desviador. Para valores principales de X’ y de X”, el modelo podría expresarse como:
y:
donde son ocho parámetros del modelo Yld2000-2D de Barlat que se identificarán con un conjunto de experimentos.
Referencias[editar]
- ↑ Weimin Han & B. Daya Reddy, pp. 55-60
- ↑ Weimin Han & B. Daya Reddy, pp. 151-172
- ↑ Tresca, H. (1864). Mémoire sur l'écoulement des corps solides soumis à de fortes pressions. C. R. Acad. Sci. Paris, vol. 59, p. 754.
- ↑ Guest
- ↑ Burzyński, W. (1929). Über die Anstrengungshypothesen. Schweizerische Bauzeitung, 94 (21), pp. 259–262.
- ↑ Yagn, Yu. I. (1931). New methods of strength prediction (in Russ.: Novye metody pascheta na prochnost'). Vestnik inzhenerov i tekhnikov, 6, pp. 237–244.
- ↑ Altenbach, H., Kolupaev, V.A. (2014) Classical and Non-Classical Failure Criteria, in Altenbach, H., Sadowski, Th., eds., Failure and Damage Analysis of Advanced Materials, in press, Springer, Heidelberg (2014), pp. 1–66
- ↑ Beljaev, N. M. (1979). Strength of Materials. Mir Publ., Moscow
- ↑ Bolchoun, A., Kolupaev, V. A., Altenbach, H. (2011) Convex and non-convex yield surfaces (in German: Konvexe und nichtkonvexe Fließflächen), Forschung im Ingenieurwesen, 75 (2), pp. 73–92
- ↑ Huber, M. T. (1904). Specific strain work as a measure of material effort (in Polish: Właściwa praca odkształcenia jako miara wytężenia materyału), Czasopismo Techniczne, Lwów, Organ Towarzystwa Politechnicznego we Lwowie, v. 22. pp. 34-40, 49-50, 61-62, 80-81
- ↑ Föppl, A., Föppl, L. (1920). Drang und Zwang: eine höhere Festigkeitslehre für Ingenieure. R. Oldenbourg, München
- ↑ Burzyński, W. (1929). Über die Anstrengungshypothesen. Schweizerische Bauzeitung 94(21):259–262
- ↑ Kuhn, P. (1980). Grundzüge einer allgemeinen Festigkeitshypothese, Auszug aus Antrittsvorlesung des Verfassers vom 11. Juli, 1980 Vom Konstrukteur und den Festigkeitshypothesen. Inst. für Maschinenkonstruktionslehre, Karlsruhe
- ↑ Kolupaev, V.A., Moneke M., Becker F. (2004). Stress appearance during creep. Calculation of plastic parts (in German: Spannungsausprägung beim Kriechen: Berechnung von Kunststoffbauteilen). Kunststoffe 94(11):79–82
- ↑ a b c d e f g Kolupaev, V.A. (2018). Equivalent Stress Concept for Limit State Analysis, Springer, Cham.
- ↑ Kolupaev, V. A., (2006). 3D-Creep Behaviour of Parts Made of Non-Reinforced Thermoplastics (in German: Dreidimensionales Kriechverhalten von Bauteilen aus unverstärkten Thermoplasten), Diss., Martin-Luther-Universität Halle-Wittenberg, Halle-Saale
- ↑ Memhard, D,., Andrieux, F., Sun, D.-Z., Häcker, R. (2011) Development and verification of a material model for prediction of containment safety of exhaust turbochargers, 8th European LS-DYNA Users Conference, Strasbourg, May 2011, 11 p.
- ↑ DiMaggio, F.L., Sandler, I.S. (1971) Material model for granular soils, Journal of the Engineering Mechanics Division, 97(3), 935-950
- ↑ Khan and Huang. (1995), Continuum Theory of Plasticity. J.Wiley.
- ↑ Neto, Periç, Owen. (2008), The mathematical Theory of Plasticity. J.Wiley.
- ↑ Podgórski, J. (1984). Limit state condition and the dissipation function for isotropic materials, Archives of Mechanics 36(3), pp. 323-342.
- ↑ a b Ivlev, D. D. (1959). The theory of fracture of solids (in Russ.: K teorii razrusheniia tverdykh tel), J. of Applied Mathematics and Mechanics, 23(3), pp. 884-895.
- ↑ a b Sayir, M. (1970). Zur Fließbedingung der Plastizitätstheorie, Ingenieur-Archiv 39(6), pp. 414-432.
- ↑ Ottosen, N. S. (1975). Failure and Elasticity of Concrete, Danish Atomic Energy Commission, Research Establishment Risö, Engineering Department, Report Risö-M-1801, Roskilde.
- ↑ Capurso, M. (1967). Yield conditions for incompressible isotropic and orthotropic materials with different yield stress in tension and compression, Meccanica 2(2), pp. 118--125.
- ↑ Lemaitre J., Chaboche J.L. (1990). Mechanics of Solid Materials, Cambridge University Press, Cambridge.
- ↑ Candland C.T. (1975). Implications of macroscopic failure criteria which are independent of hydrostatic stress, Int. J. Fracture 11(3), pp. 540–543.
- ↑ Haythornthwaite R.M. (1961). Range of yield condition in ideal plasticity, Proc ASCE J Eng Mech Div, EM6, 87, pp. 117–133.
- ↑ a b c Rosendahl, P. L., Kolupaev, V A., Altenbach, H. (2019). Extreme Yield Figures for Universal Strength Criteria, in Altenbach, H., Öchsner, A., eds., State of the Art and Future Trends in Material Modeling, Advanced Structured Materials STRUCTMAT, Springer, Cham, pp. 259-324.
- ↑ Rosendahl, P. L. (2020). From bulk to structural failure: Fracture of hyperelastic materials, Diss., Technische Universität Darmstadt.
- ↑ Szwed, A. (2000). Strength Hypotheses and Constitutive Relations of Materials Including Degradation Effects, (in Polish: Hipotezy Wytężeniowe i Relacje Konstytutywne Materiałów z Uwzględnieniem Efektów Degradacji), Praca Doctorska, Wydział Inąynierii Lądowej Politechniki Warszawskiej, Warszawa.
- ↑ Lagzdin, A. (1997). Smooth convex limit surfaces in the space of symmetric second-rank tensors, Mechanics of Composite Materials, 3(2), 119-127.
- ↑ Yu M.-H. (2002). Advances in strength theories for materials under complex stress state in the 20th century, Applied Mechanics Reviews, 55(5), pp. 169-218.
- ↑ Bigoni, D. Nonlinear Solid Mechanics: Bifurcation Theory and Material Instability. Cambridge University Press, 2012 . ISBN 9781107025417.
- ↑ Bigoni, D. and Piccolroaz, A., (2004), Yield criteria for quasibrittle and frictional materials, International Journal of Solids and Structures 41, 2855–2878.
- ↑ Podgórski, J. (1984). Limit state condition and the dissipation function for isotropic materials. Archives of Mechanics, 36 (3), pp. 323–342.
- ↑ Piccolroaz, A. and Bigoni, D. (2009), Yield criteria for quasibrittle and frictional materials: a generalization to surfaces with corners, International Journal of Solids and Structures 46, 3587–3596.
- ↑ Altenbach, H., Bolchoun, A., Kolupaev, V.A. (2013). Phenomenological Yield and Failure Criteria, in Altenbach, H., Öchsner, A., eds., Plasticity of Pressure-Sensitive Materials, Serie ASM, Springer, Heidelberg, pp. 49–152.
- ↑ Kolupaev, V.A. (2018). Equivalent Stress Concept for Limit State Analysis, Springer, Cham.
Bibliografía[editar]
- Weimin Han & B. Daya Reddy: Plasticity: Mathematical Theory and Numerical Analysis, Springer-Verlag, Nueva York, 1999, ISBN 0-387-98704-5.









![{\displaystyle \gamma _{1}=\gamma _{2}\in ]0,1[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66ab6f7a14a52c2042d17030aa16705df21f1541)
![{\displaystyle \gamma _{1}\in ]0,1[,\gamma _{2}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab67fc470c16fd7d16b50462f9c9d7af9b70f566)

![{\displaystyle \gamma _{1}=-\gamma _{2}\in ]0,1[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19f234ad4d2cddbc2eb4b2b5c0dfcb2a128c275b)

![{\displaystyle \gamma _{1}\in ]0,1[,\gamma _{2}<0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc95c96fba08cb97251ef453346323702300f9ab)
![{\displaystyle \gamma _{1}\in ]0,1[,\gamma _{2}\in ]0,\gamma _{1}[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bdf157e5b65de316f3462bcb5e2de9d10cda1cb)






![{\displaystyle \nu _{+}^{\mathrm {in} }\in {\bigg [}\,0.48,\,{\frac {1}{2}}\,{\bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b7c270b90d3c766fd6ecd9b7204e1622d9f7722)
![{\displaystyle \nu _{+}^{\mathrm {in} }\in ]-1,~\nu _{+}^{\mathrm {el} }\,]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/690096f2ce81fb70324e3cebefabb993721ed772)

![{\displaystyle 3\,I_{2}'=\left\{{\begin{array}{ll}\displaystyle {\frac {\sigma _{\mathrm {eq} }-\gamma _{1}\,I_{1}}{1-\gamma _{1}}}\,{\frac {\sigma _{\mathrm {eq} }+\gamma _{1}\,I_{1}}{1+\gamma _{1}}},&I_{1}>0\\[1em]\displaystyle {\frac {\sigma _{\mathrm {eq} }}{1-\gamma _{1}}}\,{\frac {\sigma _{\mathrm {eq} }}{1+\gamma _{1}}},&I_{1}\leq 0\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84e5badc1256fedb02c6e3bb4e32c3c04f455c74)


![{\displaystyle \nu _{+}^{\mathrm {in} }\in \left]-1,\,1/2\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0492b09eaa5450be7f96f4a04b025a37ef0a620)


![{\displaystyle \nu _{+}^{\mathrm {in} }\in [0.48,1/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95b2a945c4242aba4b539c51f5dc7441fceda3b9)
![{\displaystyle \gamma _{1}\in [0,0.1155]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bee6b21ec154dddb4479a8f5fc3321c72ec824f4)





![{\displaystyle 3\,I_{2}'=\left\{{\begin{array}{ll}\displaystyle {\frac {\sigma _{\mathrm {eq} }-\gamma _{1}\,I_{1}}{1-\gamma _{1}}}\,{\frac {\sigma _{\mathrm {eq} }-\gamma _{2}\,I_{1}}{1-\gamma _{2}}},&I_{1}>-d\,\sigma _{\mathrm {+} }\\[1em]\displaystyle {\frac {\sigma _{\mathrm {eq} }^{2}}{(1-\gamma _{1}-\gamma _{2})^{2}}},&I_{1}\leq -d\,\sigma _{\mathrm {+} }\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7665d54a30d98465586f222a2ad1cf088bfd4d2a)






















![{\displaystyle S_{yc}={\tfrac {1}{\sqrt {2}}}\left[(\sigma _{1}-\sigma _{2})^{2}+(\sigma _{2}-\sigma _{3})^{2}+(\sigma _{3}-\sigma _{1})^{2}\right]^{1/2}-c_{0}-c_{1}~(\sigma _{1}+\sigma _{2}+\sigma _{3})-c_{2}~(\sigma _{1}+\sigma _{2}+\sigma _{3})^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/168ce31fef86a9a05a75721a81e088c69edcf24f)












![{\displaystyle \Omega _{3}(\theta ,\beta _{3},\chi _{3})=\cos \left[\displaystyle {\frac {1}{3}}\left(\pi \beta _{3}-\arccos[\,\sin(\chi _{3}\,{\frac {\pi }{2}})\,\!\cos 3\,\theta \,]\right)\right],\qquad \beta _{3}\in [0,\,1],\quad \chi _{3}\in [-1,\,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31655f9e540e841ea6d966f7a0bdbe1fd6304b4a)
![{\displaystyle \beta _{3}=[0,\,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20634c0926a05259beda78f4e18b1ea6d38621be)





![{\displaystyle \chi _{3}=[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b4456eca66f88480bde86583de8ac126d973ac4)

![{\displaystyle \Omega _{6}(\theta ,\beta _{6},\chi _{6})=\cos \left[\displaystyle {\frac {1}{6}}\left(\pi \beta _{6}-\arccos[\,\sin(\chi _{6}\,{\frac {\pi }{2}})\,\!\cos 6\,\theta \,]\right)\right],\qquad \beta _{6}\in [0,\,1],\quad \chi _{6}\in [-1,\,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e980c867fa1766fcc5a741ecf363e19c05a8bfe8)
![{\displaystyle \beta _{6}=[0,\,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61f7b566943062df913486ad99edfa445fbb58a1)















![{\displaystyle F(p)=\left\{{\begin{array}{ll}-Mp_{c}{\sqrt {(\phi -\phi ^{m})[2(1-\alpha )\phi +\alpha ]}},&\phi \in [0,1],\\+\infty ,&\phi \notin [0,1],\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9948aa54df1e39ab115e425b19f088dff39beadc)


![{\displaystyle g(\theta )={\frac {1}{\cos[\beta {\frac {\pi }{6}}-{\frac {1}{3}}\cos ^{-1}(\gamma \cos 3\theta )]}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dba97f3c7548243d55f4c6736d862e34b31b04cb)





















![{\displaystyle \left[{\begin{array}{*{20}{c}}{{L'}_{11}}\\{{L'}_{12}}\\{{L'}_{21}}\\{{L'}_{22}}\\{{L'}_{66}}\end{array}}\right]=\left[{\begin{array}{*{20}{c}}{2/3}&0&0\\{-1/3}&0&0\\0&{-1/3}&0\\0&{-2/3}&0\\0&0&1\end{array}}\right]\left[{\begin{array}{*{20}{c}}{\alpha _{1}}\\{\alpha _{2}}\\{\alpha _{7}}\end{array}}\right],\left[{\begin{array}{*{20}{c}}{{L''}_{11}}\\{{L''}_{12}}\\{{L''}_{21}}\\{{L''}_{22}}\\{{L''}_{66}}\end{array}}\right]=\left[{\begin{array}{*{20}{c}}{-2}&2&8&{-2}&0\\1&{-4}&{-4}&4&0\\4&{-4}&{-4}&4&0\\{-2}&8&2&{-2}&0\\0&0&0&0&1\end{array}}\right]\left[{\begin{array}{*{20}{c}}{\alpha _{3}}\\{\alpha _{4}}\\{\alpha _{5}}\\{\alpha _{6}}\\{\alpha _{8}}\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ad31d6027e7e5da286c1ec7579505cffa4c919c)
